背景
因为入职不久,最近在接手一个外卖的分配问题,即在一个区域同时产生多个订单,且该区域有多个骑手,在只考虑一个骑手只能接一单的情况下,订单与骑手之间到底应该如何分配。在第一版解决方案中我们使用的是匈牙利算法,目前还在测试当中,还没有上线,希望其能有不错的效果。写此博客,专门为了好好了解其基本原理,而不是只会按部就班用现成的库,而根本不懂其原理。
匈牙利算法原理
在了解匈牙利算法之前,首先需要掌握几个图论中的基本概念。
二分图:在图论中,二分图是一类特殊的图,又称为双分图、二部图、偶图。二分图的顶点可以分成两个互斥的独立集U和V的图,使得所有边都是连结一个U中的点和一个V中的点。顶点集 U、V 被称为是图的两个部分。等价的,二分图可以被定义成图中所有的环都有偶数个顶点。

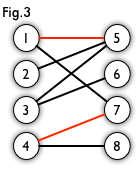
匹配:在图论中,一个「匹配」(matching)是一个边的集合,其中任意两条边都没有公共顶点。例如,图 3、图 4 中红色的边就是图 2 的匹配。
 |
 |
 |
 |
我们定义匹配点、匹配边、未匹配点、非匹配边,它们的含义非常显然。例如Fig.3中 1、4、5、7 为匹配点,其他顶点为未匹配点;1-5、4-7为匹配边,其他边为非匹配边。
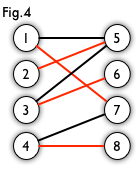
最大匹配:一个图所有匹配中,所含匹配边数最多的匹配,称为这个图的最大匹配。图 4 是一个最大匹配,它包含 4 条匹配边。
完美匹配:如果一个图的某个匹配中,所有的顶点都是匹配点,那么它就是一个完美匹配。图 4 是一个完美匹配。显然,完美匹配一定是最大匹配(完美匹配的任何一个点都已经匹配,添加一条新的匹配边一定会与已有的匹配边冲突)。但并非每个图都存在完美匹配。
增广路径
交替路:从一个未匹配点出发,依次经过非匹配边、匹配边、非匹配边…形成的路径叫交替路。
增广路:从一个未匹配点出发,走交替路,如果途径另一个未匹配点(出发的点不算),则这条交替路称为增广路(agumenting path)。例如,图 5 中的一条增广路如图 6 所示(图中的匹配点均用红色标出):
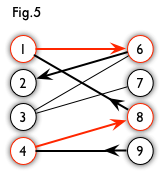
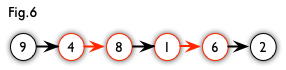
增广路有一个重要特点:非匹配边比匹配边多一条。因此,研究增广路的意义是改进匹配。只要把增广路中的匹配边和非匹配边的身份交换即可。由于中间的匹配节点不存在其他相连的匹配边,所以这样做不会破坏匹配的性质。交换后,图中的匹配边数目比原来多了1条。我们可以通过不停地找增广路来增加匹配中的匹配边和匹配点。找不到增广路时,达到最大匹配(这是增广路定理。
暴力递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
res = 0
def brute_force(arr):
if len(arr) == 0:
print('the input array format is not right')
return
path = 0
used = [False] * len(arr[0])
helper(arr, 0, used, path)
return res
def helper(arr, row, used, path):
if row == len(arr):
global res
res = max(res, path)
for i in range(0, len(used)):
if used[i]:
continue
used[i] = True
if arr[row][i]:
path += 1
helper(arr, row+1, used, path)
used[i] = False
if arr[row][i]:
path -= 1
if __name__ == '__main__':
arr = [[0, 0, 1, 1, 1], [0, 0, 1, 0, 1], [0, 1, 1, 0, 1], [0, 1, 0, 0, 0], [0, 1, 1, 1, 0]]
res = brute_force(arr)
print(res)
dfs算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
# @Time : 10/12/19 17:05
# @Author : xcTorres
# @FileName: hungarian.py
class Hungarian(object):
def _hungarian(self, x):
# 遍历每个worker
for i in range(self.m):
#如果相连且该工人还没有访问过,即还没有放入至增广路径
if self.arr[x][i] == 1 and not self.visited[i]:
self.visited[i] = True
#若该工人还没有分配到工作, 或者找到增广路径,就分配新的工作给工人。
if self.match[i] == -1 or self._hungarian(self.match[i]) == 1:
self.match[i] = x
print("{}->{}".format(x, i))
return True
else:
return False
'''
arr is 2-d array,
of which the size is m*n
we can regard row as jobs,
col as workers,
'''
def solve(self, arr):
if len(arr) == 0:
print('the input numpy array format is not right')
return
self.arr = arr
self.m = len(arr)
self.n = len(arr[0])
#每个工人是否分配到任务
self.match = [-1] * self.n
path = 0
# 遍历每个job,
for i in range(self.m):
self.visited = [False] * self.n
print('start to match:', i)
if self._hungarian(i):
path += 1
return path
if __name__ == '__main__':
arr = [[0, 1, 1, 0], [1, 1, 0, 0], [1, 0, 0, 0], [0, 0, 0, 1]]
hungarian = Hungarian()
path = hungarian.solve(arr)
print(path)
"""
start to match: 0
0->1
start to match: 1
1->0
start to match: 2
0->2
1->1
2->0
start to match: 3
3->3
4
"""
数学角度
在实际生产环境中,dfs方式还是很少用到,多是转换成矩阵操作, 那么其数学原理是什么呢? 首先匈牙利算法可以抽象成如下数学问题。即代价矩阵C乘以一个特殊矩阵X,其中X中每行或者每一列都是单位向量,即1处在不同行不同列.
$\min z=\sum\limits_{i=1}^n\sum\limits_{j=1}^n c_{ij}x_{ij}$
$ \mathrm{s.t}\begin{cases}\sum\limits_{i=1}^n x_{ij}=1,\quad i=1,2,\cdots,n \\ \sum\limits_{j=1}^n x_{ij}=1,\quad j=1,2,\cdots,n \\ x_{ij}=0 或 1, \quad i,j=1,2,\cdots,n \end{cases} $
-
定理一
从下图可以看出,对一个代价矩阵C,无论是同一行加上同样的值或者是同一列加上同样的值。不会影响最终目标函数$ \min z=\sum\limits_{i=1}^n\sum\limits_{j=1}^n c_{ij}x_{ij} $的优化结果, 因为乘以不同的元素矩阵X得到的组合最后都会生成一个元素总和相同的矩阵。

-
定理二
且对另一个非负矩阵,可以知道其最优解的结果一定大于等于0,若能够找到一组独立的零元素解,则其必定为最优解。其解释如下图。
在定理一,二的基础上。匈牙利算法则有了以下解法。
1) 给定一个代价矩阵
2) 通过给行加减相同的值,或者给列相加减相同的值,最优解元素矩阵X不会发生变化
3) 一直进行相应操作,直至找到在保证非负矩阵的前提下独立零元素的一组解。
这些步骤还存在一些细节,即如何快速找到独立零元素, 如何判定找到的零元素就是独立零元素。 该链接有比较详细的六步走步骤,如果感兴趣的话,可以研究一下哦。http://csclab.murraystate.edu/~bob.pilgrim/445/munkres.html。这是从数学的角度来看如何解匈牙利分配问题,也是非常的精妙。且在性能上更高,如下有一些官方的库,供推荐。
补充:
scipy库的最新的linear_sum_assignment根据新论文更新了算法,效率得到了显著提升,不亚于lapsolver和lap。可直接使用。
https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.linear_sum_assignment.html
参考
https://www.renfei.org/blog/bipartite-matching.html
https://www.geeksforgeeks.org/hungarian-algorithm-assignment-problem-set-1-introduction/
https://keson96.github.io/2016/08/29/2016-08-29-Assignment-Problem-And-Hungrian-Method/
https://www.youtube.com/watch?v=rrfFTdO2Z7I
http://longrm.com/2018/05/05/2018-05-05-KM/
https://luzhijun.github.io/2016/10/10/%E5%8C%88%E7%89%99%E5%88%A9%E7%AE%97%E6%B3%95%E8%AF%A6%E8%A7%A3/