Dijkstra算法是图算法中，寻找两个节点最短路径的算法。在路网做路径规划中，也常常用到该算法的变种。
基本思想
- 通过Dijkstra计算图G中的最短路径时，需要指定起点s(即从顶点s开始计算)。
- 此外，引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度)，而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。
- 初始时，S中只有起点s；U中是除s之外的顶点，并且U中顶点的路径是”起点s到该顶点的路径”。然后，从U中找出路径最短的顶点，并将其加入到S中；接着，更新U中的顶点和顶点对应的路径。 然后，再从U中找出路径最短的顶点，并将其加入到S中；接着，更新U中的顶点和顶点对应的路径。 … 重复该操作，直到遍历完所有顶点。
伪代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
function Dijkstra(Graph, source):
dist[source] ← 0
create vertex priority queue Q
for each vertex v in Graph:
if v ≠ source:
dist[v] ← INFINITY
Q.add_with_priority(v, dist[v])
while Q is not empty:
u ← Q.extract_min()
for each neighbor v of u:
if dist[u] + length(u, v) < dist[v]:
dist[v] = dist[u] + length(u, v)
Q.decrease_priority(v, dis[v])
return dis
优先队列能够提高运行效率，其时间复杂度为$O(E + Vlog(V))$，这里E代表图的总边个数，V代表图的总顶点个数。从伪代码不难看出，需要维护一个数组，用来存储每一个node的当前最短路径距离，source node初始化为0，其他为$\infty$ ；并将这些点载入到优先队列，优先值为当前最短路径距离；source node初始化为0，其余nodes为无穷大。此后便不停pop 最短路径距离最小的结点。
示例
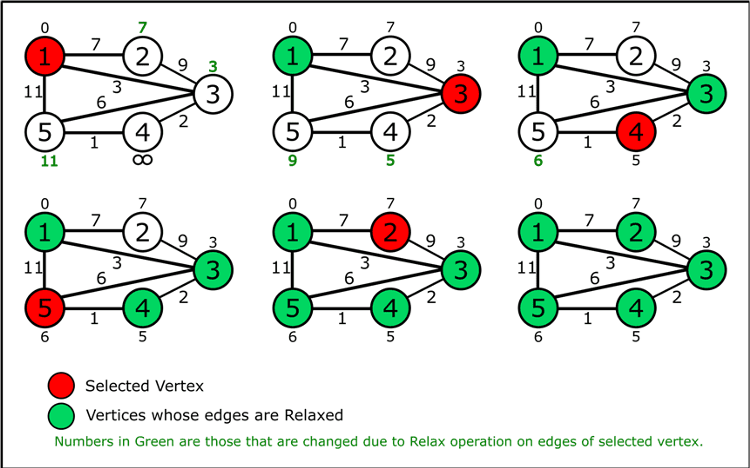我们来看一个示例，node 1为源结点：
- 1) 在第一次迭代中， 源节点最短路径距离为0，所以被弹出。其所有neighbour(node 2,3,5)的最短路径距离根据公式$dist[v] = dist[u] + length(u, v) （if\;dist[u] + length(u, v) < dist[v])$都被更新，由于node 4不与node 1相连，所以其最短路径距离仍为$\infty$
- 2) 在第二次跌代中，在剩余nodes中，node 3的最短路径距离为3最小，则被弹出。其所有neighbour(node 2,4, 5)的最短路径距离更新
- 3）在第三次迭代中，node 4最短距离为5，被弹出。
- 4）剩余的迭代都是同样的道理