当谈论到两点之间的路径规划算法,我们首先想到的是Dijkstra算法,为了提升效率又改进出现了Bidirectional Dijkstra算法。但对于国家,大陆级别的道路网规模,查询效率还是太慢,甚至超过2s,很难达到ms级的响应。而本文将介绍的Contraction Hierarchies算法即是在原始Graph先进行预处理,提前先算好一些点与点之间的最短路径距离(Shortcuts),简化Graph的Edge个数,再利用改进的Bidirection Dijkstra找到最短路径。
Node Importance
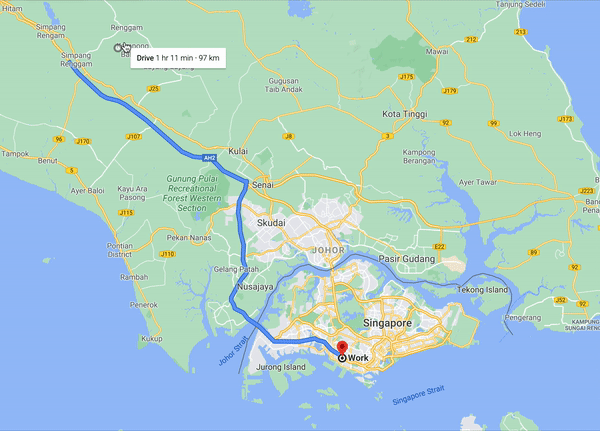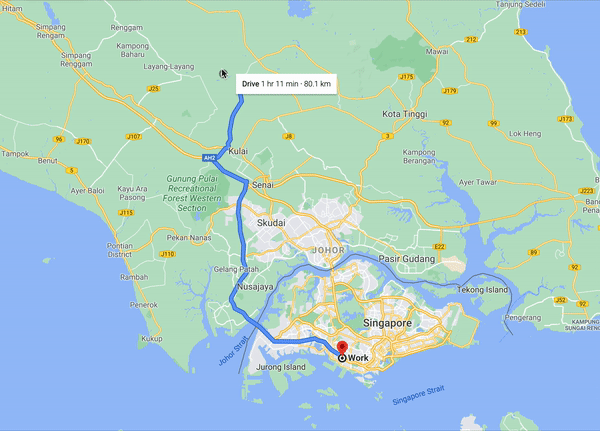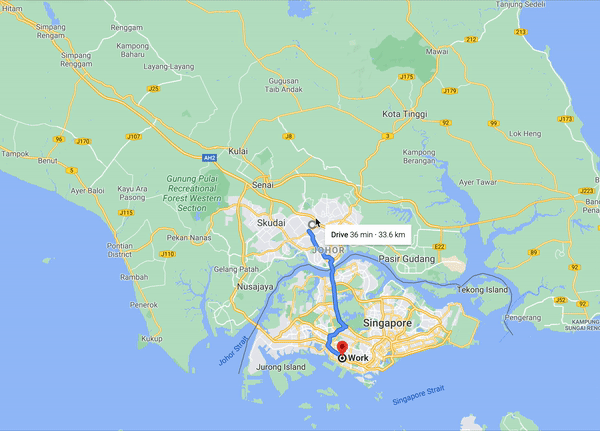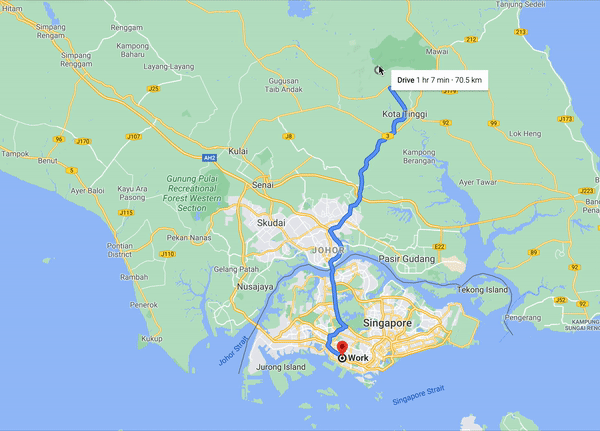
首先我们先来介绍Node重要度。给定一个有很多vertex和Edge的路网Graph,当我们计算各个顶点之间的最短路径的时候我们会发现一个现象,很多对顶点的最短路径都会必须经过一些“重要”的节点,如上图如果我们想计算新加坡的各个点到马来西亚点的最短路径,两座大桥上的顶点是必经之地。当我们开启一段长途旅行的时候,可以抽象为如下的行程。
- 在当地的公路上开往最近的一条高速公路的入口
- 持续的在高速公路上行驶,直至驶出高速公路
- 在当地的公路行驶,开往目的地。
Shortcut
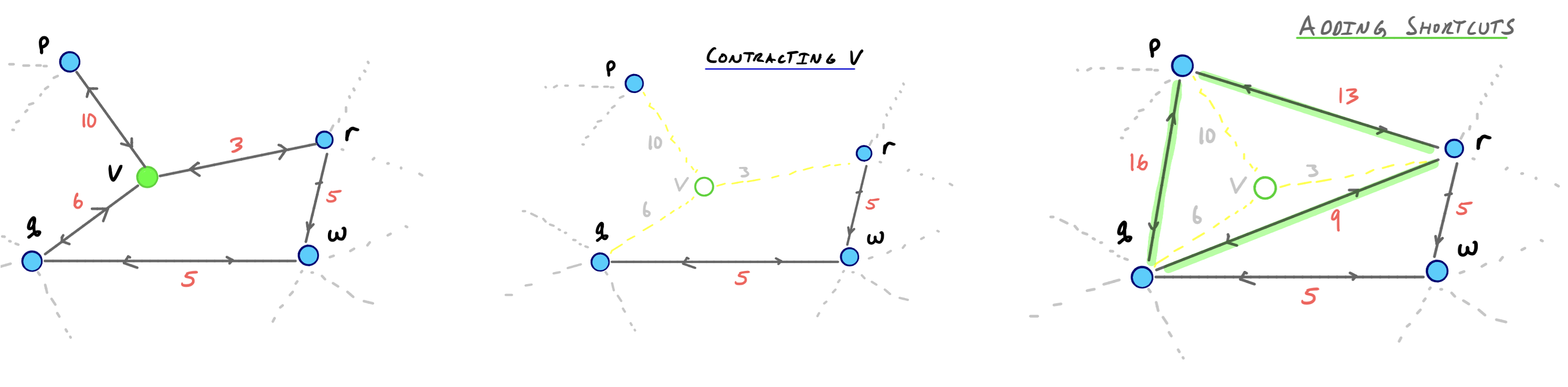
不难发现,高速公路,大桥的顶点似乎重要度比较高。那怎么量化这种重要度呢,需要再来介绍一下Shortcuts,它是CH算法预处理中很关键的步骤,也是因为提前算好一些点与点之间的最短距离,添加Shortcut之后,在搜索中简化Graph的复杂度。从下图我们可以看到,顶点p到顶点r,顶点q到顶点r,顶点p到q的最短路径都会经过顶点v,而假设v不存在,则可以加上pq,qr,pr三条Shortcuts。
而重要度的计算公式也是基于Shortcut的,也叫Edge Difference,其中$Edge Difference= shortcuts - incoming edges - outgoing edges$, 也就是所添加的Shortcut个数减去其本身连接的Edge个数。
针对刚刚的例子,点v的重要度就是3 - 3 - 3 = -3。所以像高速公路,或者一些重要公路上的顶点,由于他们影响着很多点与点之间的最短路径,假设他们消失的话,就得加上很多Shortcuts,他们的Edge Difference也就会非常大。CH算法原始论文中,证明以任意一种顺序给node排序,并一一添加Shortcut都保证最后最短路径结果的准确性;但通过重要度从低到高排序,添加Shortcut可以保证添加的Shortcut尽可能的少,双向搜索效率更高。
Bidirectional Search
按照重要度顺序添加Shortcuts的步骤也叫Contraction,经过这一步骤最后得到的预处理的Graph即是原始的Graph,添加了一些Shortcuts。这样看来整个Graph的Edge不减反增,那又是如何做到减少时间复杂度而提升效率的呢,原因在于CH算法是在特定的部分图,而不是直接在预处理的图做双向Dijkstra算法。这种特殊的图叫Upward Graph,即图里面的每条边上的两个点都是从重要度从低指向高。
当做Bidirectoinal Dijkstra的时候,是从起点开始的Upward Graph开始搜索,同时从终点的Downward Graph开始搜索,直至他们相遇在某点。此时Upward Graph是高度简化的grpah,边的个数大大减少,从而大大提高搜索效率。
这时的双向搜索就好比在预处理中我先算好各个城市,县城,乡村中的小路到最近的大路,高速公路的最短距离,等真正计算长途A,B的最短路径距离时,我们只需要尽可能知道A与其最近的高速公路的入口的最短距离,B与其最近高速公路出口的最短距离,再加上高速公路本身的距离,就可以很快计算出A与B之间的最短距离。我们来看个例子,如下图中的右上图是原始Graph加上三条红色的Shortcuts,
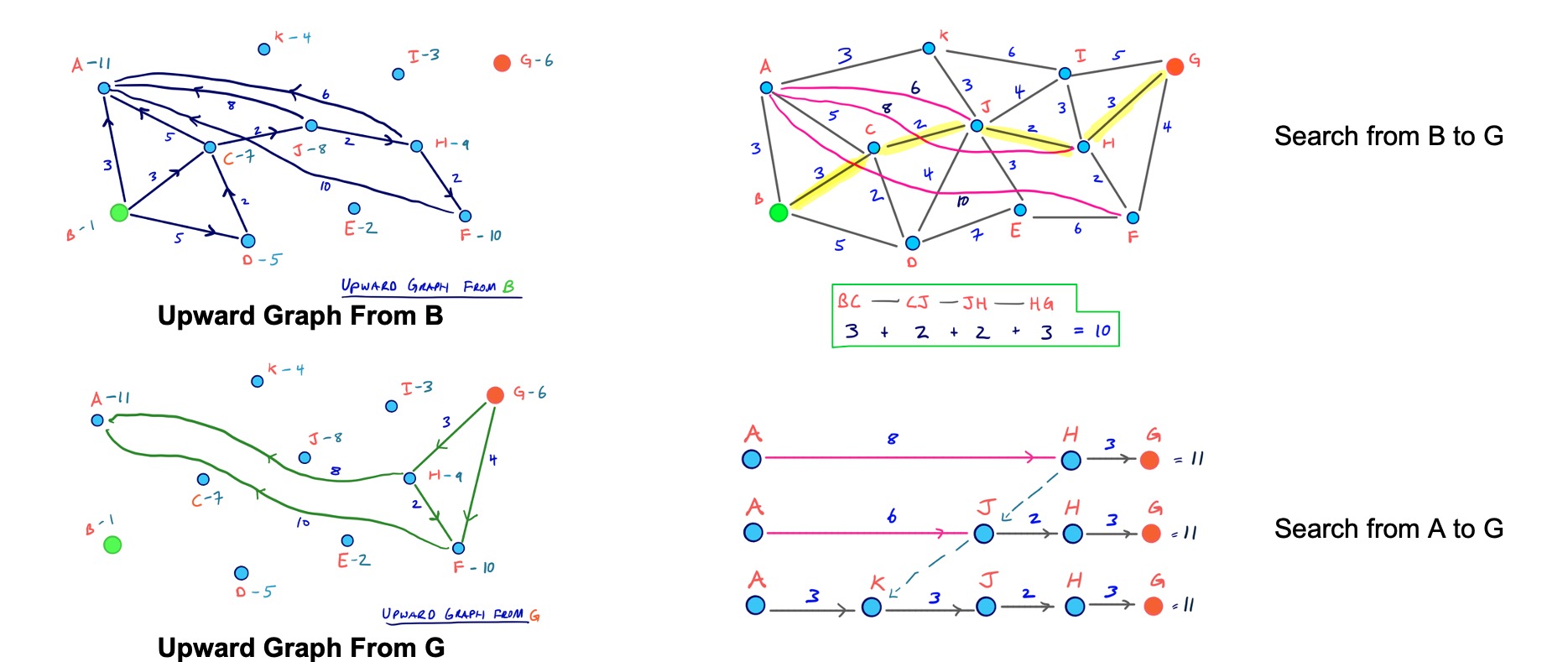
1)Search from B to G
当我们计算B到G的最短路径时,首先得到从B开始的Upward graph,以及从G开始的Upward graph,分别列在下图左列的两个子图。最终可以发现他们相遇与H点,则最短路径为B->C->J->H->G。
2)Search from A to G
当我们计算A到G的最短路径时,A已经是重要度最高的node了,所以没有从A开始的Upward graph了,只能使用从G开始的Upward graph。从Upward Graph From G不难发现,A->H->G就是最短路径,可以很快得到最短距离是3+8=11,但是最短路径中A->H是一条Shortcut,想要得到真实路径需要unpack,得到最终最短为A->K->J->H->G。
Reference
https://courses.cs.washington.edu/courses/cse332/20wi/homework/contraction/
https://jlazarsfeld.github.io/ch.150.project/sections/10-ch-query/
https://github.com/navjindervirdee/Advanced-Shortest-Paths-Algorithms
https://github.com/Project-OSRM/osrm-backend
https://www.coursera.org/lecture/algorithms-on-graphs/highway-hierarchies-and-node-importance-HV35U